Teoria Moderna del Portafoglio: la nascita dell'Asset Allocation

«A good portfolio is more than a long list of good stocks and bonds. It is a balanced whole, providing the investor with protections and opportunities with respect to a wide range of contingencies».

Harry Markowitz

L'Asset Allocation rappresenta uno dei concetti fondamentali nella gestione finanziaria e trova le sue radici nel lavoro pionieristico di Harry Markowitz.

Nel 1952, Markowitz pubblicò il suo rivoluzionario articolo intitolato "Portfolio Selection", in cui gettava le basi per quella che sarebbe divenuta nota come la Modern Portfolio Theory (MPT), ovvero la Teoria Moderna del Portafoglio.

La Teoria Moderna del Portafoglio ha introdotto un approccio scientifico alla costruzione e alla gestione dei portafogli di investimento, enfatizzando l'importanza della diversificazione per ottimizzare il rapporto tra rischio e rendimento.

Markowitz dimostrò che, attraverso una combinazione di strumenti finanziari con rischi non perfettamente correlati, è possibile ridurre la volatilità complessiva del portafoglio, senza necessariamente sacrificare il rendimento atteso. Questa teoria ha trasformato radicalmente il modo in cui gli investitori e i professionisti della finanza concepiscono la gestione del rischio e la creazione di valore nel lungo periodo.

L'evoluzione dell'Asset Allocation, a partire dai principi della Teoria Moderna del Portafoglio, continua a influenzare profondamente le strategie di investimento contemporanee, rendendo il contributo di Markowitz ancora attuale e di primaria importanza nel campo della finanza.

Indice

1. Introduzione
2. Rischio e rendimento di un portafoglio di due strumenti finanziari rischiosi
3. Rischio e rendimento di un portafoglio rischioso con investimento in uno strumento privo di rischio
4. Rischio e rendimento di un portafoglio di più di due strumenti finanziari rischiosi
5. Il portafoglio tangente e l'indice di Sharpe

1. Introduzione

«Portfolio theory, as used by most financial planners, recommends that you diversify with a balance of stocks and bonds and cash that's suitable to your risk tolerance».

Harry Markowitz

Markowitz fu il primo studioso a formalizzare matematicamente la nozione di diversificazione degli investimenti, un concetto che da quel momento in poi cominciò a delinearsi come una strategia fondamentale nella gestione dei portafogli, anche se ci vorrà del tempo prima che la diversificazione diventi una prassi comune.

Attraverso il processo di Asset Allocation e grazie ai vantaggi offerti dalla diversificazione, è possibile ridurre il rischio complessivo di un portafoglio senza compromettere il rendimento atteso. Questo principio rappresenta uno dei pilastri della Modern Portfolio Theory.

Markowitz definì il rischio come la varianza dei rendimenti. Scegliendo la giusta combinazione di strumenti finanziari e bilanciando opportunamente i loro pesi, è possibile identificare un portafoglio efficiente per ogni livello di rendimento atteso: quello che minimizza la varianza dei rendimenti, e quindi il rischio.

L'aspetto più rivoluzionario del lavoro di Markowitz fu il passaggio dall'analisi dei singoli titoli alla considerazione del portafoglio nel suo complesso. Non è tanto il rischio intrinseco di un singolo strumento a essere determinante, quanto piuttosto il modo in cui quel singolo strumento contribuisce al rischio complessivo del portafoglio, misurato attraverso la varianza totale.

In altre parole, la covarianza tra un singolo strumento e gli altri componenti del portafoglio assume un ruolo cruciale nella determinazione del rischio complessivo.

Questa innovazione è di fondamentale importanza: la decisione di includere un determinato titolo non dipenderà più semplicemente dal confronto del suo rendimento e della sua varianza con quelli di altri titoli, quanto da quali altri strumenti l’investitore vorrà includere nel proprio portafoglio.

In questo articolo, applicheremo il processo di ottimizzazione sviluppato da Markowitz sia a esempi teorici che a casi pratici, utilizzando serie storiche dei rendimenti di strumenti finanziari reali, per mostrare concretamente come la Modern Portfolio Theory possa essere implementata nella gestione degli investimenti.

2. Rischio e rendimento di un portafoglio di due strumenti finanziari rischiosi

«Diversifying sufficiently among uncorrelated risks can reduce portfolio risk toward zero. But financial engineers should know that's not true of a portfolio of correlated risks».

Harry Markowitz

Si suppone che l'investitore utilizzi interamente la propria disponibilità finanziaria per l'investimento.

Il rendimento di un portafoglio formato da due titoli, denominati a e b, è pari alla media ponderata dei rendimenti dei due titoli in base ai rispettivi pesi:

\begin{equation} r_p = x_ar_a + x_br_b \end{equation}

Dove:
r_p = Rendimento del portafoglio.
r_a = Rendimento del primo titolo.
r_b = Rendimento del secondo titolo.
x_a = Peso del primo titolo.
x_b = 1 – x_a = Peso del secondo titolo.

Il calcolo della varianza del portafoglio, che utilizziamo come misura del rischio, è invece più complesso.

Essa è data dalla seguente formula:

\begin{equation} σ_p^2 = x_a^2σ_a^2 + x_b^2σ_b^2 + 2x_ax_bσ_{ab} \end{equation}

Dove:
σ_p² = Varianza dei rendimenti del portafoglio.
σ_a² = Varianza dei rendimenti del primo titolo.
σ_b² = Varianza dei rendimenti del secondo titolo.
σ_ab = Covarianza tra i rendimenti del primo e del secondo titolo.

Per ottenere la deviazione standard del portafoglio (σ_p), è sufficiente estrarre la radice quadrata della varianza:

\begin{equation} \sigma_p=\sqrt{\sigma_p^2} \end{equation}

A differenza del rendimento atteso, la deviazione standard del portafoglio non è semplicemente una media ponderata delle deviazioni standard dei due titoli. Questo perché entra in gioco la covarianza tra i titoli a e b, che può essere positiva, negativa o nulla, a seconda di come i rendimenti di a e b si muovono in relazione tra loro.

È particolarmente interessante analizzare i casi estremi in cui la correlazione lineare tra i due titoli assume i valori +1, −1 e 0, poiché questi scenari offrono intuizioni importanti sulla struttura del rischio del portafoglio.

Da questo punto in avanti, ogni riferimento alla correlazione si riferirà sempre alla correlazione lineare tra i rendimenti dei titoli.

Correlazione = +1. La relazione grafica tra il rendimento atteso e la deviazione standard del portafoglio è la seguente:

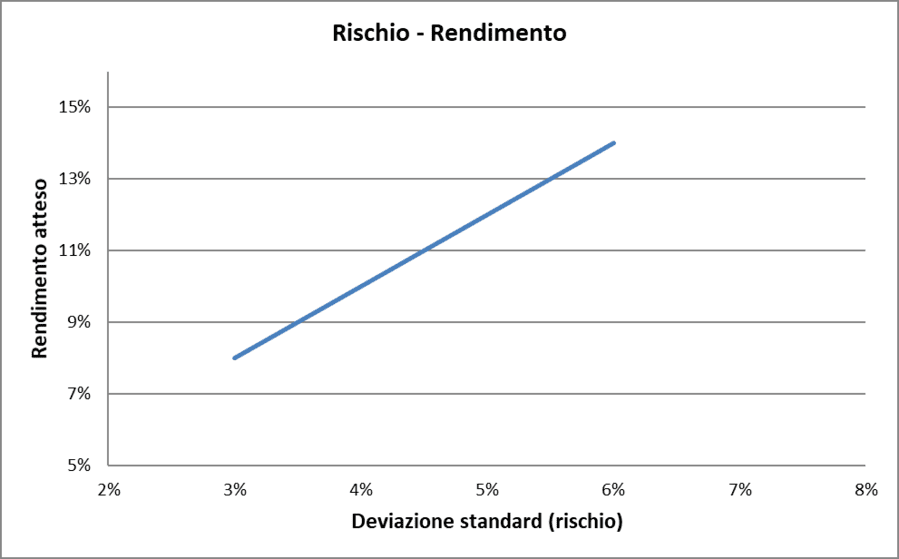
Rischio/Rendimento con correlazione = 1 (caso teorico)

La linea blu sul grafico rappresenta i livelli di rischio (misurati dalla deviazione standard) e rendimento atteso di un portafoglio composto da due titoli con una correlazione lineare perfettamente positiva, pari quindi a +1:

• Punto più in basso a sinistra. Questo punto sulla linea blu corrisponde a un portafoglio composto al 100% dal titolo a. In questo caso, la deviazione standard del portafoglio è del 3%, mentre il rendimento atteso è dell'8%.
• Punto più in alto a destra. Questo punto identifica un portafoglio composto al 100% dal titolo b. Qui, la deviazione standard è del 6% e il rendimento atteso è del 14%.

I punti lungo la linea blu rappresentano tutte le possibili combinazioni dei due titoli a e b. Ad esempio, un portafoglio potrebbe essere composto per il 10% dal titolo a e per il 90% dal titolo b, o per il 20% dal titolo a e per l'80% dal titolo b, e così via. Ogni combinazione di pesi tra a e b produce un punto specifico sulla linea, determinando il rischio e il rendimento atteso di quel particolare portafoglio.

Quando la correlazione tra i due titoli è perfettamente positiva:

• La deviazione standard di un portafoglio è semplicemente una media ponderata delle deviazioni standard dei singoli titoli, calcolata sulla base degli stessi pesi utilizzati per il rendimento atteso. Questo implica che la formula per il rischio del portafoglio non beneficia della diversificazione: la varianza non viene ridotta.
• In pratica, detenere due titoli con una correlazione di +1 non offre alcun vantaggio in termini di riduzione del rischio. La deviazione standard del portafoglio rimane invariata rispetto a quella dei singoli titoli, calcolata in proporzione al peso di ciascun titolo nel portafoglio.

Caso reale

Nella realtà, è estremamente raro trovare due titoli con una correlazione dei rendimenti esattamente pari a +1, a meno che non si stiano confrontando due titoli che siano praticamente identici, differenziati solo per la classe o per le commissioni applicate.

Il nostro obiettivo è stato quello di identificare una coppia di fondi con rendimenti altamente correlati, avvicinandosi il più possibile a una correlazione di +1, pur senza raggiungere questo valore teorico.

Il portafoglio è stato costruito utilizzando i seguenti fondi: Fonditalia Equity Italy R e Interfund Equity Italy Acc, entrambi appartenenti alla categoria degli "Azionari Italia" e gestiti in modo attivo. Per una comprensione più approfondita delle differenze tra fondi a gestione attiva e passiva, si consiglia di leggere l'articolo È meglio investire in fondi a gestione attiva o passiva?

L'analisi copre il periodo dal 30 maggio 2016 al 23 maggio 2017, comprendendo un totale di 256 giorni borsistici. Durante questo intervallo temporale, la correlazione tra i rendimenti dei due fondi è risultata essere di +0,9892, un valore molto vicino alla correlazione perfetta di +1, ma non esattamente identico.

Questo risultato riflette una relazione quasi perfettamente lineare tra i rendimenti dei due fondi, il che li rende un caso di studio ideale per esaminare le dinamiche di un portafoglio con correlazione positiva molto alta.

La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio, in funzione delle diverse combinazioni di peso tra i due titoli nel portafoglio, è la seguente:

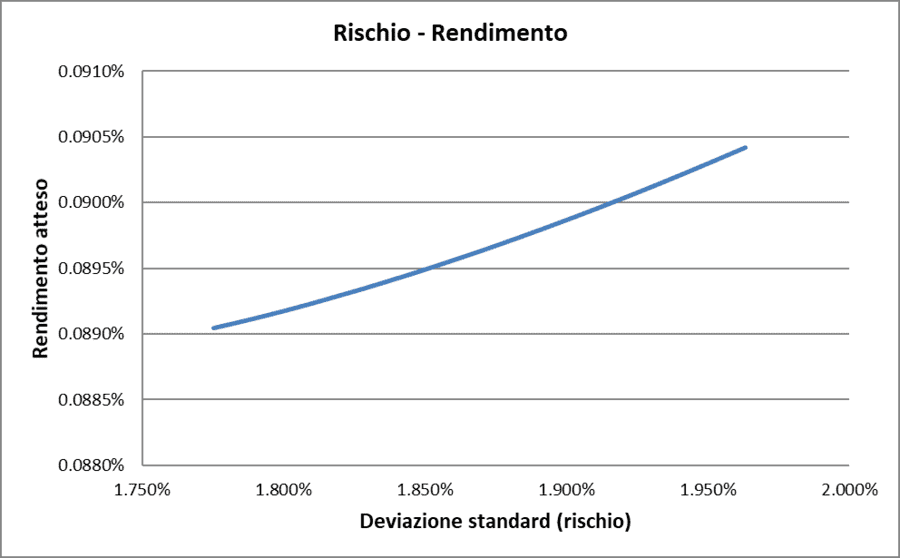
Rischio/Rendimento con correlazione = 1 (caso reale)

La curva risultante è leggermente arcuata, ma nel complesso molto simile a quella osservata nel grafico teorico per una correlazione perfetta di +1.

Questo riflette il fatto che, nonostante la correlazione non sia esattamente +1, i rendimenti dei due fondi si muovono in modo sincronizzato, riducendo al minimo i benefici della diversificazione.

Correlazione = −1. Quando la correlazione lineare tra i rendimenti di due titoli è pari a −1, la relazione grafica tra il rendimento atteso e la deviazione standard del portafoglio assume una configurazione particolare:

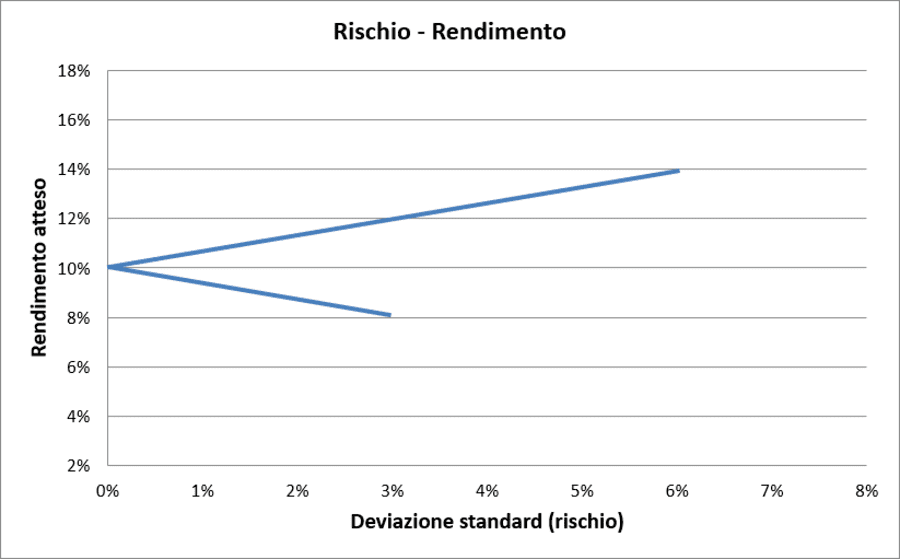
Rischio/Rendimento con correlazione = −1 (caso teorico)

In questa situazione teorica, è possibile individuare una combinazione dei due titoli in cui il rischio del portafoglio si annulla completamente. Ciò significa che esiste una specifica allocazione di pesi tra i due titoli che, grazie alla correlazione perfettamente negativa, permette di azzerare la varianza del portafoglio.

In altre parole, la diversificazione raggiunge il suo massimo potenziale: l'eliminazione totale del rischio pur mantenendo un rendimento atteso che si colloca tra i rendimenti dei due titoli.

Questa condizione ideale rappresenta un esempio perfetto della potenza della diversificazione.

Purtroppo, nella pratica è estremamente difficile, se non impossibile, trovare due strumenti finanziari con una correlazione dei rendimenti pari a −1. Nel mondo reale, le correlazioni negative sono infatti molto più rare di quelle positive, specialmente a questo livello estremo.

Anche se non si può eliminare completamente il rischio, una buona diversificazione può comunque migliorare significativamente il rapporto tra rendimento e rischio.

Un portafoglio ben diversificato è in grado di generare un rendimento atteso per unità di rischio (misurato come varianza o deviazione standard) superiore rispetto a quello che si otterrebbe investendo nei singoli strumenti finanziari presi singolarmente.

Caso reale

Il portafoglio è stato costruito utilizzando i seguenti fondi: Fideuram Italia e UBI Pramerica – Obbligazioni Globali.

Il primo fondo è classificato come azionario italiano, mentre il secondo appartiene alla categoria degli obbligazionari globali in euro. L'analisi si riferisce al periodo compreso tra il 30 maggio 2016 e il 23 maggio 2017, per un totale di 256 giorni borsistici.

In questo intervallo di tempo, la correlazione tra i rendimenti dei due fondi è risultata essere pari a −0,6015. Sebbene non raggiunga il valore teorico di −1, questa correlazione negativa indica che i rendimenti dei due fondi tendono a muoversi in direzioni opposte, seppure non in modo perfettamente inverso.

La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio, considerando le varie combinazioni di peso tra i due fondi, è la seguente:

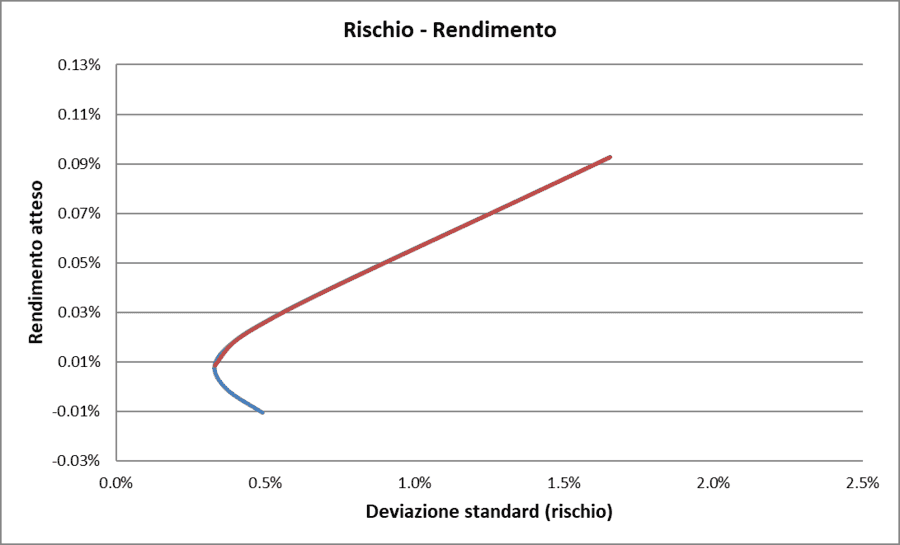
Rischio/Rendimento con correlazione = −1 (caso reale)

Anche se ci discostiamo dal caso teorico di correlazione perfetta pari a −1, è fondamentale osservare che esiste una combinazione dei due fondi che consente di ottenere un rischio inferiore rispetto a ciascun fondo considerato singolarmente. Inoltre, questa combinazione permette di raggiungere un rendimento atteso superiore a quello del fondo con il rendimento più basso.

Questo dimostra l'efficacia della diversificazione nel ridurre il rischio del portafoglio, pur migliorando il rendimento atteso.

Osservando il grafico, possiamo iniziare a distinguere il concetto di portafoglio efficiente. La parte rossa della curva rappresenta l'insieme dei portafogli efficienti, cioè le combinazioni dei due fondi che offrono il miglior equilibrio possibile tra rischio e rendimento. Questi portafogli sono considerati ottimali perché, per ogni livello di rischio, offrono il massimo rendimento atteso possibile.

La porzione rossa della curva viene definita "frontiera efficiente".

Un portafoglio efficiente è caratterizzato dal fatto che non può essere migliorato né in termini di rendimento atteso né in termini di rischio. Esistono certamente portafogli che offrono un rendimento atteso superiore, ma questi comportano anche un rischio maggiore. Al contrario, ci sono portafogli con un rischio inferiore, ma che presentano un rendimento atteso più basso.

Un portafoglio efficiente rappresenta la soluzione ottimale per ogni livello di rischio, minimizzandolo per il rendimento atteso desiderato.

La scelta tra diversi portafogli efficienti dipenderà da fattori soggettivi, come la propensione individuale al rischio e le aspettative di rendimento dell'investitore.

Per ogni investitore, il portafoglio efficiente sarà quello situato sulla frontiera efficiente, con un livello di rischio atteso che rispecchia la propria tolleranza al rischio. Questa scelta permette di ottimizzare la propria strategia d'investimento in funzione delle proprie esigenze e aspettative.

Correlazione = 0. Quando la correlazione lineare tra i rendimenti di due titoli è pari a 0, la rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio è la seguente:

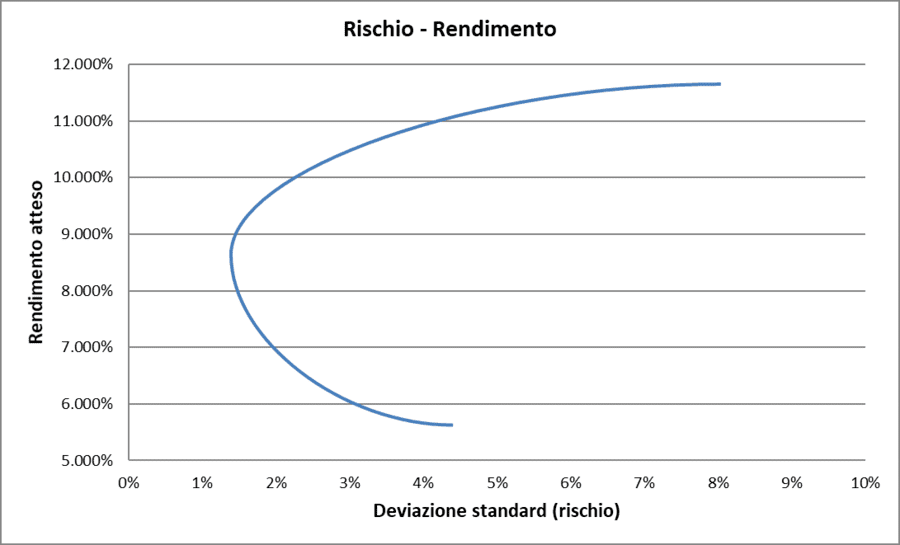
Rischio/Rendimento con correlazione = 0 (caso teorico)

In questo scenario, anche se non è possibile azzerare completamente il rischio del portafoglio, esistono combinazioni di titoli che possono ridurre il rischio rispetto a quello dei singoli titoli presi separatamente.

La mancanza di correlazione (correlazione pari a zero) tra i rendimenti dei due titoli indica che i loro movimenti di prezzo sono indipendenti l'uno dall'altro. Ciò consente di beneficiare della diversificazione, riducendo il rischio complessivo del portafoglio, anche se non al livello massimo possibile come nel caso di correlazione negativa.

Caso reale

Il portafoglio è stato costruito utilizzando i seguenti fondi: BG Selection SICAV – Anima Italy Equities AX e Investec Global Strategy Fund – UK Alpha Fund F Acc USD.

Il primo fondo è un azionario italiano, mentre il secondo è un azionario del Regno Unito, denominato in dollari, con un focus sulle società a grande capitalizzazione. L'analisi copre il periodo dal 30 maggio 2016 al 23 maggio 2017, comprendente 256 giorni borsistici.

La correlazione tra i rendimenti dei due fondi nel periodo considerato è risultata pari a −0,0041, un valore leggermente negativo ma estremamente vicino a zero. Questo indica che i rendimenti dei due fondi sono stati praticamente indipendenti tra loro.

La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio, considerando le diverse combinazioni di peso tra i due titoli, è la seguente:

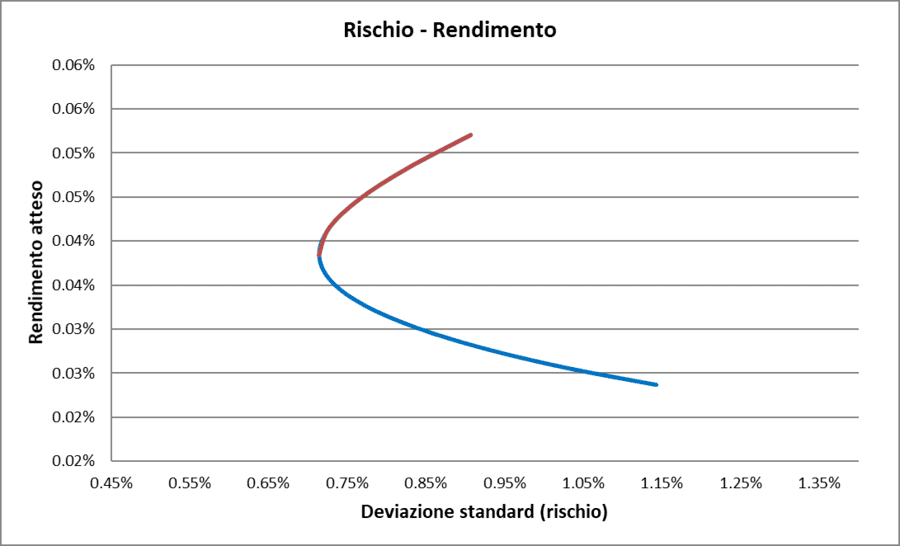
Rischio/Rendimento con correlazione = 0 (caso reale)

Anche in questo caso, la parte rossa della curva rappresenta la frontiera efficiente, ovvero l'insieme dei portafogli ottimali che offrono il miglior compromesso tra rischio e rendimento dei due fondi.

Per riassumere le diverse situazioni di correlazione, possiamo utilizzare un grafico che sintetizza in un'unica immagine tutte le relazioni precedentemente analizzate:

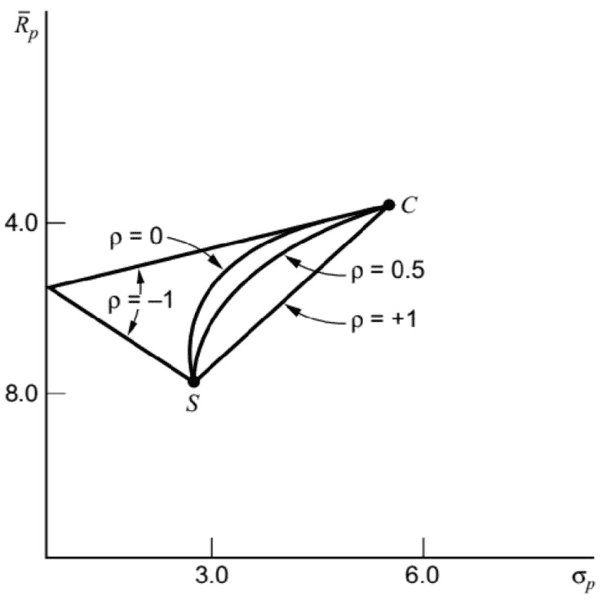
Rischio/rendimento (tutti i casi)

La regione compresa tra i punti C, S e il punto in cui i segmenti toccano l’asse y individua i portafogli ammissibili che possono essere creati combinando due titoli, a seconda della correlazione lineare tra i rendimenti dei titoli stessi.

Soltanto alcuni di questi portafogli sono considerati efficienti, in base ai criteri esaminati in precedenza: si tratta di quelli che si trovano lungo la frontiera efficiente, rappresentando le scelte ottimali per gli investitori che desiderano massimizzare il rendimento atteso per un dato livello di rischio o minimizzare il rischio per un dato rendimento atteso.

3. Rischio e rendimento di un portafoglio rischioso con investimento in uno strumento privo di rischio

«I would never be 100 percent in stocks or 100 percent in bonds or cash».

Harry Markowitz

Un investimento privo di rischio viene definito "risk free". In realtà, nessun investimento è completamente esente da rischi: per quanto basso, ogni portafoglio e ogni strumento finanziario possiede un certo grado di rischio.

Nel mondo reale, si fa spesso riferimento ai titoli di Stato, ai Buoni Fruttiferi Postali, ai conti correnti con un massimale garantito di 100.000 euro e ad altri strumenti simili come investimenti considerati privi di rischio.

Il rendimento atteso di un portafoglio rischioso, denominato come r_pf, in cui non si investe l'intero capitale ma si riserva una parte a uno strumento privo di rischio (c), è calcolato come segue:

\begin{equation} r_{pf}=x_pr_p+\left(1-x_p\right)r_c=r_c + x_p\left(r_p-r_c\right) \end{equation}

Dove:
r_pf = Rendimento del portafoglio che include anche il titolo privo di rischio.
r_p = Rendimento del portafoglio rischioso.
r_c = Rendimento dello strumento privo di rischio.
x_p = Peso del portafoglio rischioso.

Il rendimento del portafoglio rischioso, in cui una parte del capitale è investita in uno strumento privo di rischio, non è altro che una media ponderata tra il rendimento del portafoglio rischioso e quello dello strumento privo di rischio.

Riorganizzando la formula, possiamo interpretare il risultato come il rendimento dello strumento privo di rischio, al quale si aggiunge il differenziale di rendimento tra il portafoglio rischioso e il rendimento privo di rischio (r_p − r_c), moltiplicato per il peso del portafoglio rischioso (x_p).

Questa interpretazione è particolarmente interessante: il differenziale tra il rendimento del portafoglio rischioso e quello privo di rischio è chiamato premio per il rischio o rendimento in eccesso. Questo è l'extra rendimento che un investitore è disposto ad accettare per allocare una parte del proprio capitale in un investimento rischioso.

Per quanto riguarda la varianza del portafoglio, considerando che lo strumento privo di rischio ha varianza (σ_c²) e covarianza con il portafoglio rischioso (σ_pc) pari a zero, la formula si semplifica così:

\begin{equation} σ_{pf}^2 = x_p^2σ_p^2 + (1 - x_p)σ_c^2 + 2x_p(1 - x_p)σ_{pc} = x_p^2σ_p^2 \end{equation}

Per calcolare la deviazione standard del portafoglio (σ_pf), sarà sufficiente estrarre la radice quadrata della varianza:

\begin{equation} \sigma_{pf}=\sqrt{x_p^2σ_p^2}=x_pσ_p \end{equation}

La varianza del nuovo portafoglio dipende quindi soltanto dalla parte investita nel portafoglio rischioso.

Graficamente:

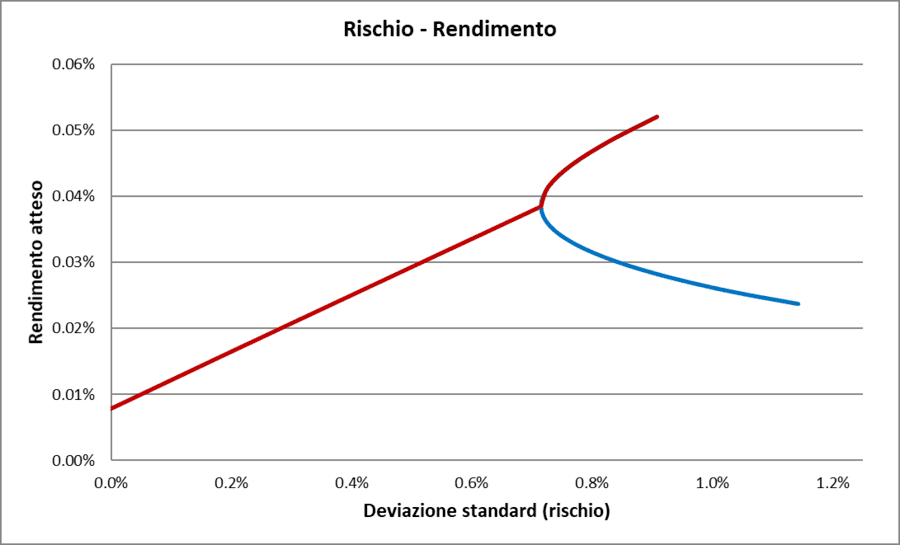
Rischio/Rendimento con investimento privo di rischio

La parte rossa della curva rappresenta la frontiera efficiente.

La retta sul grafico rappresenta tutte le possibili combinazioni di rischio e rendimento di un portafoglio composto dai fondi BG Selection SICAV – Anima Italy Equities AX (60% della parte rischiosa) e Investec Global Strategy Fund – UK Alpha Fund F Acc USD (40% della parte rischiosa), insieme a un investimento privo di rischio. L'analisi si basa sullo stesso periodo di riferimento.

I pesi assegnati ai due fondi, rispettivamente 60% e 40%, non sono casuali: individuano il portafoglio efficiente col minor rischio.

La curva, invece, rappresenta le possibili combinazioni di rischio e rendimento nel caso in cui l'intero capitale sia investito esclusivamente nel portafoglio rischioso, senza alcuna allocazione a uno strumento privo di rischio.

4. Rischio e rendimento di un portafoglio di più di due strumenti finanziari rischiosi

«The chief problem with the individual investor: he or she typically buys when the market is high and thinks it's going to go up, and sells when the market is low and thinks it's going to go down».

Harry Markowitz

Caso reale

Il portafoglio in esame è stato costruito utilizzando i seguenti fondi: Fonditalia Equity Italy R, Investec Global Strategy Fund – UK Alpha Fund F Acc USD e UBI Pramerica – Obbligazioni Globali. Questi fondi sono stati già analizzati in precedenza, e la loro combinazione offre un'interessante opportunità per esplorare le dinamiche di un portafoglio diversificato con più di due strumenti finanziari.

Il periodo di analisi rimane invariato: dal 30 maggio 2016 al 23 maggio 2017, per un totale di 256 giorni borsistici.

Le correlazioni tra i rendimenti dei fondi durante il periodo in esame sono le seguenti:

• 0,477 tra Fonditalia e Investec.
• −0,3563 tra Fonditalia e UBI.
• −0,3387 tra Investec e UBI.

Questi valori di correlazione indicano che i fondi hanno una relazione non perfettamente lineare tra di loro, con una correlazione positiva e due negative. Ciò implica che la diversificazione attraverso questi fondi può offrire benefici in termini di riduzione del rischio complessivo del portafoglio.

La rappresentazione grafica della relazione tra il rendimento atteso e la deviazione standard del portafoglio, considerando le diverse combinazioni di peso tra i tre fondi, è la seguente:

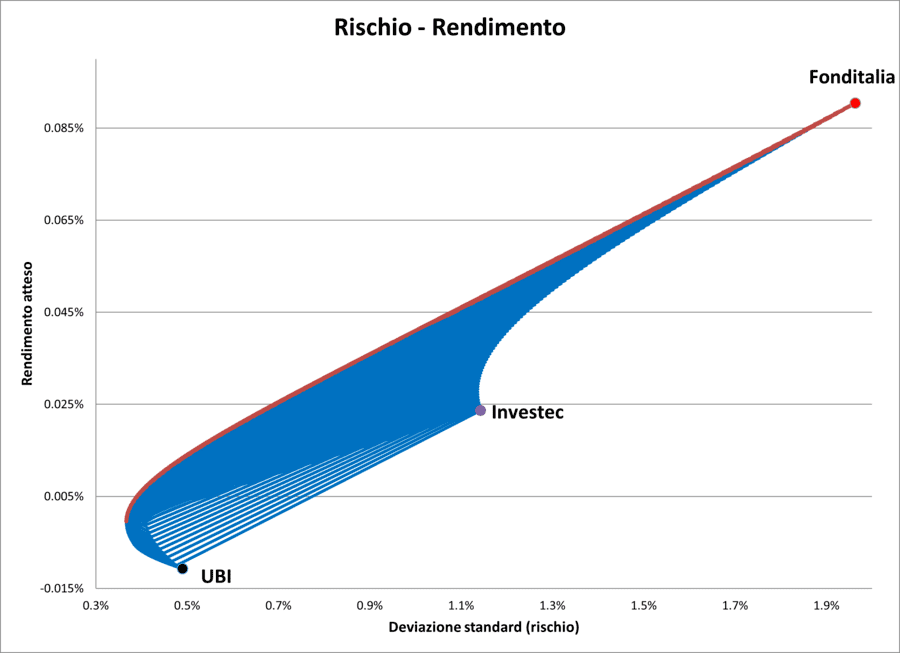
Rischio/Rendimento (caso reale con 3 fondi)

In questo caso, il grafico non presenta una semplice curva, ma un'area composta da una moltitudine di punti, ciascuno dei quali rappresenta una combinazione specifica di rischio-rendimento. La parte rossa, situata lungo il bordo superiore di questa regione blu, rappresenta la frontiera efficiente.

Il grafico è stato creato considerando un totale di 5.151 punti (combinazioni di rischio e rendimento atteso), ottenuti calcolando la volatilità e il rendimento per tutte le possibili combinazioni di pesi tra i tre fondi analizzati. Il gap tra i pesi è stato del solo 1%, il che ha permesso di considerare una vasta gamma di possibili combinazioni, come ad esempio 0-0-100%, 1-0-99%, 1-1-98%, e così via.

Di questi 5.151 punti, 675 si trovano sulla frontiera efficiente e individuano i portafogli che offrono il massimo rendimento possibile per ciascun livello di rischio.

Il grafico evidenzia anche i livelli di rischio e rendimento atteso generati dai portafogli composti al 100% da ciascuno dei tre fondi individualmente. È interessante notare che solo uno di questi portafogli, quello composto interamente da Fonditalia, si trova sulla frontiera efficiente, precisamente nel punto associato al massimo rendimento e al maggior rischio.

Questo suggerisce che, se questi tre fondi costituissero l'intero universo di opzioni di investimento disponibili, un investitore con una forte propensione al rischio avrebbe teoricamente scelto il portafoglio efficiente costituito dal 100% di Fonditalia.

Tuttavia, lo stesso non si può dire per gli altri due fondi (UBI e Investec): investire l'intero capitale in uno di essi non rappresenterebbe una soluzione efficiente, poiché esistono molte altre combinazioni di investimento tra i tre fondi che, a parità di rischio, offrono rendimenti superiori.

Se la stessa analisi fosse effettuata utilizzando un diverso insieme di fondi o un diverso periodo di analisi, le conclusioni potrebbero variare significativamente.

In generale, l'aumento del numero di titoli o fondi all'interno di un portafoglio tende a migliorare la frontiera efficiente. Un maggior numero di opzioni di investimento consente una diversificazione più ampia, che può portare a una riduzione del rischio del portafoglio senza sacrificare il rendimento atteso, o alternativamente, a un aumento del rendimento atteso senza incrementare il rischio complessivo del portafoglio.

5. Il portafoglio tangente e l'indice di Sharpe

«You can’t predict, but you can prepare».

Howard Marks

Abbiamo visto in precedenza come il rendimento di un portafoglio rischioso, in cui una parte del capitale è investita in uno strumento privo di rischio, possa essere espresso come una media ponderata tra il rendimento del portafoglio rischioso e quello dello strumento privo di rischio.

Graficamente, questo si traduce in una retta che rappresenta tutte le possibili combinazioni di rischio e rendimento per un portafoglio misto composto da fondi rischiosi e un investimento privo di rischio.

Ora riprendiamo questo concetto con alcune differenze:

• Il portafoglio è composto da tre fondi, anziché due.
• La retta non interseca la frontiera efficiente nel punto di minima volatilità, ma sarà tangente ad essa.
• Si ipotizza che la retta intersechi l’asse delle ordinate al livello di rendimento offerto da un investimento privo di rischio.

Il punto di tangenza tra la retta e la frontiera efficiente identifica quello che viene chiamato portafoglio tangente. Questo portafoglio è particolarmente importante perché rappresenta il portafoglio efficiente che, combinato con un investimento privo di rischio, offre il miglior rendimento aggiustato per il rischio.

La pendenza della retta che passa per il portafoglio tangente è nota come l'indice di Sharpe, ed è calcolata come:

\begin{equation} Indice\ di\ Sharpe=\frac{Rendimento\ in\ eccesso\ del\ portafoglio}{Volatilità\ del\ portafoglio} \end{equation}

Più precisamente, esso si calcola nel modo seguente:

\begin{equation} Indice\ di\ Sharpe=\frac{r_p-r_f}{\sigma_p} \end{equation}

Dove:
r_p = Rendimento del portafoglio.
r_f = Tasso di rendimento a rischio zero.
σ_p = Volatilità del portafoglio.

L’Indice di Sharpe misura il rapporto tra il premio per il rischio (ovvero, il rendimento in eccesso rispetto a un investimento privo di rischio) e la volatilità di un portafoglio. Questo indice viene massimizzato quando il portafoglio efficiente scelto è proprio il portafoglio tangente.

Tutti gli altri portafogli rischiosi lungo la frontiera efficiente (e, naturalmente, anche quelli inefficienti) si troveranno al di sotto della retta tangente.

Il coefficiente angolare di questa retta rappresenta l'Indice di Sharpe, indicando che il portafoglio tangente è quello che offre il rendimento più elevato per unità di volatilità rispetto a qualsiasi altro portafoglio disponibile.

Questo concetto può essere rappresentato graficamente come segue:

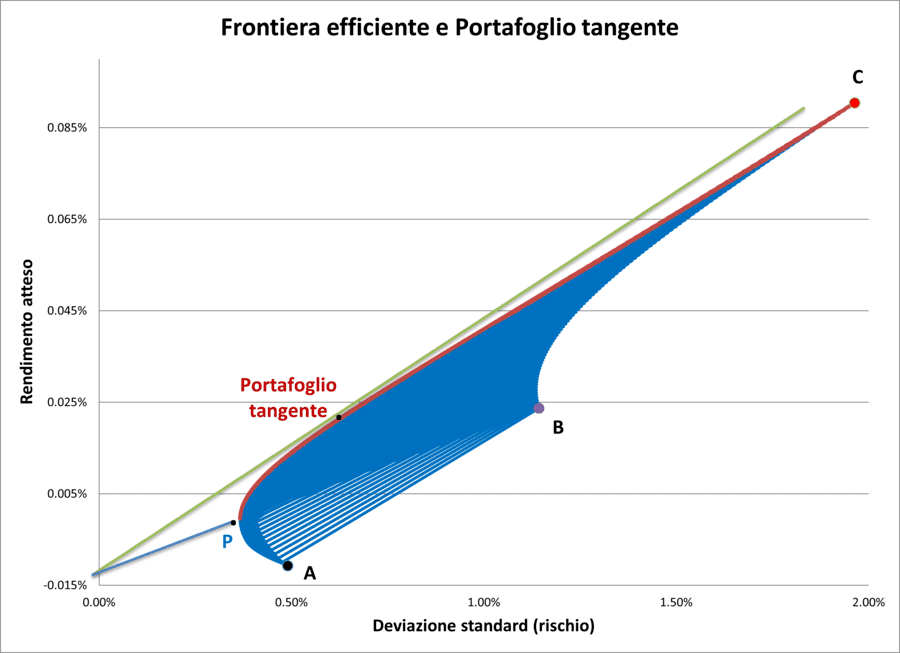
Portafoglio tangente

Il portafoglio tangente è quindi considerato il miglior portafoglio in senso assoluto, poiché massimizza il rendimento per unità di rischio. Questo concetto è fondamentale nel Capital Asset Pricing Model (CAPM), dove si passa dall'idea di una molteplicità di portafogli efficienti, basati sulla propensione al rischio dell'investitore, all'individuazione del miglior portafoglio possibile in termini oggettivi.

Quando si include un investimento privo di rischio, il portafoglio tangente diventa l'unico portafoglio rischioso efficiente. In altre parole, i portafogli efficienti ora sono quelli che possono essere ottenuti combinando l'investimento privo di rischio con il portafoglio tangente. L'intera frontiera efficiente si riduce a una linea retta, dove il portafoglio tangente rappresenta l'unico portafoglio rischioso che merita di essere considerato.

La propensione al rischio dell'investitore continua a giocare un ruolo importante, determinando la percentuale di capitale da investire nel portafoglio tangente:

• Gli investitori più aggressivi allocano una porzione maggiore del loro capitale nell'investimento rischioso, posizionandosi quindi in una zona della retta vicina al portafoglio tangente. Se decidono di investire tutto il loro capitale nel portafoglio rischioso, si posizioneranno esattamente nel punto del portafoglio tangente.
• Gli investitori più prudenti si collocano in una zona della retta vicina all'asse delle ordinate, che rappresenta il rendimento dell'investimento privo di rischio. Se decidono di investire tutto il loro capitale in strumenti non rischiosi, si posizioneranno esattamente nel punto in cui la retta interseca l'asse delle ordinate.

Il portafoglio tangente e l'Indice di Sharpe sono quindi concetti chiave non solo per la costruzione di portafogli efficienti, ma anche per la gestione del rischio e l'ottimizzazione del rendimento in un contesto di mercato reale.

La loro applicazione pratica permette agli investitori di massimizzare il rendimento del proprio portafoglio per un dato livello di rischio, fornendo una guida oggettiva alla selezione degli investimenti.

Un'interessante intervista in lingua inglese a Harry Markowitz è disponibile su Youtube: IFA.tv - An Hour with Harry Markowitz, Father of Modern Portfolio Theory.