La correlazione lineare
- Information
- Correlazione 19161 hits
- Prima pubblicazione: 17 Luglio 2018
«One of the first things taught in introductory statistics textbooks is that correlation is not causation. It is also one of the first things forgotten».
Thomas Sowell
Quando si parla di correlazione ci si riferisce generalmente al grado di relazione tra due variabili.
La più importante tipologia di correlazione è quella lineare, che viene misurata dall'indice di correlazione di Pearson o indice di correlazione lineare.
Esso può assumere valori compresi tra −1 e +1:
- Quando l'indice è positivo, esiste una correlazione lineare diretta tra le due variabili osservate; la correlazione diretta è massima al raggiungimento del valore di +1.
- Quando l'indice è negativo, esiste una correlazione lineare inversa tra le due variabili osservate; la correlazione inversa è massima al raggiungimento del valore di −1.
- Quando l'indice è uguale a 0, le due variabili osservate non presentano correlazione lineare; la correlazione lineare è assente.
La disposizione dei punti e i valori dell'indice di correlazione lineare nell'immagine seguente danno un'idea della variabilità di quest'ultimo in funzione delle possibili conformazioni dei fenomeni osservati:
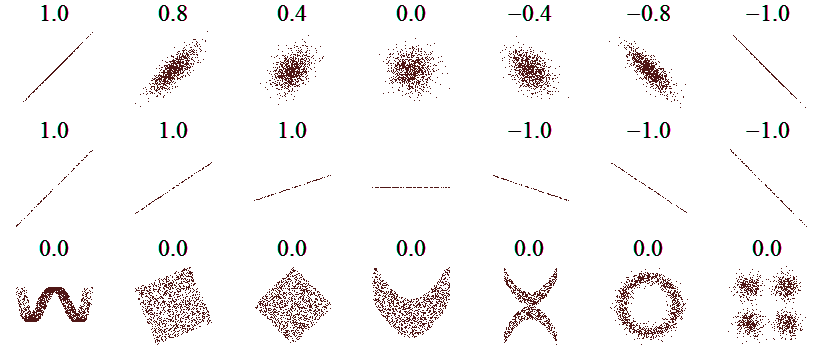
Nell'ultima riga dell'immagine le disposizioni dei punti seguono degli andamenti ben definiti e non casuali. Tuttavia, sono tutti esempi di relazioni non lineari e l'indice di correlazione lineare è pari a 0.
D'ora in poi, quando parleremo di correlazione faremo sempre riferimento alla correlazione lineare.
Indice
- Differenza tra correlazione lineare e covarianza
- Correlazione spuria
- Correlazione rolling
- Analisi di correlazione lineare di Dedalo Invest
- Parametri dell'analisi di correlazione lineare
Differenza tra correlazione lineare e covarianza

«The analysis of variance is not a mathematical theorem, but rather a convenient method of arranging the arithmetic».
Ronald Fisher
La covarianza e il coefficiente di correlazione lineare sono due misure statistiche simili ma con alcune importanti differenze.
Entrambe misurano il livello di relazione esistente tra due variabili.
La correlazione lineare è una funzione della covarianza in quanto si ottiene dividendo la covarianza delle due variabili per il prodotto delle deviazioni standard delle stesse due variabili.
Chiamiamo A la serie storica dei rendimenti dello strumento finanziario x e B quella dello strumento y.
La formula dell'indice di correlazione lineare è la seguente:
\begin{equation} \rho_{AB}=\frac{cov\left(A,B\right)}{\sigma_A\sigma_B}\end{equation}
dove cov(A, B) rappresenta la covarianza di A e B, mentre σA e σB sono, rispettivamente, le deviazioni standard di A e B.
La correlazione lineare fornisce un'informazione in più rispetto alla covarianza: mentre quest'ultima indica soltanto la direzione della relazione lineare tra due variabili, la correlazione lineare ne indica la direzione e ne misura l'intensità.
Questa caratteristica rende la correlazione lineare molto più conosciuta e utilizzata della covarianza, perché i suoi valori sono compresi in un intervallo che va da −1 a +1: sono valori standardizzati e di più facile comprensione rispetto a quelli della covarianza, che può variare da meno infinito a più infinito.
Correlazione spuria

«But to measure cause and effect... you must ensure that a simple correlation, however tempting it may be, is not mistaken for a cause. In the 1990s the stork population of Germany increased and the German at-home birth rate rose as well. Shall we credit storks for airlifting the babies?».
Neil deGrasse Tyson
La correlazione non implica una relazione di causalità tra le due variabili osservate.
Quando questa relazione di causa-effetto manca, siamo in presenza di correlazione spuria.
La correlazione, a differenza della regressione lineare, non implica l'esistenza di una variabile dipendente e una indipendente.
Purtroppo, la correlazione spuria – nella quale la casualità (e non la causalità) o una terza variabile sono alla base dei co-movimenti tra due variabili – è stata all'origine di equivoci di notevole portata.
Prendiamo ad esempio la curva di Phillips, che fu resa famosa dall'economista William Phillips nel 1958: essa misura una relazione inversa tra il tasso di inflazione e quello di disoccupazione.
Relazione inversa abbiamo detto: se queste due quantità si muovono davvero in modo inverso, significa che sono legate da una correlazione lineare inversa; l'indice di correlazione dovrebbe perciò essere negativo.
La curva di Phillips nacque dall'osservazione empirica dei movimenti opposti tra il tasso di inflazione e quello di disoccupazione e, soltanto in seguito, fu costruito un modello matematico a supporto dei dati osservati.
A partire dagli anni '70 del secolo scorso, il modello ha smesso di funzionare: la correlazione inversa tra i due tassi è sovente venuta meno.
Come avviene spesso in casi del genere, nuovi e più sofisticati modelli hanno cercato di spiegare le anomalie verificatesi: nessuno di essi si è però imposto in modo definitivo.
Le opinioni non sono unanimi e rimane il forte dubbio che la curva di Phillips sia stata originata da una correlazione spuria.
In un libro molto divertente e di facile lettura, intitolato Spurious correlations, Tyler Vigen ha presentato numerosi esempi di correlazione spuria. Vediamone alcuni:
- Perdite economiche causate dal crimine informatico e utili per azione della società inglese Domino Pizza tra il 2003 e il 2009: indice di correlazione lineare = 0,98.
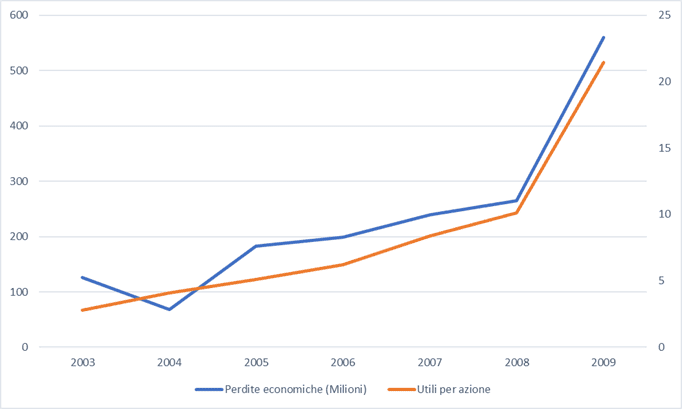
- Posizione nella classifica degli show più visti della CBS della sitcom "Due uomini e mezzo" e indice NYSE Composite tra il 2005 e il 2011 (valori annuali): indice di correlazione lineare = 0,95.
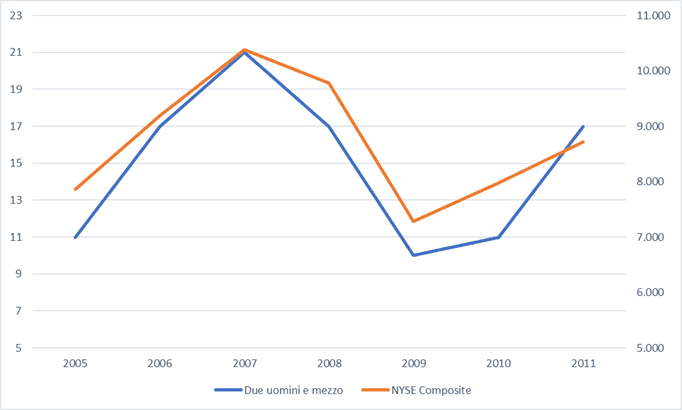
- Libri di filosofia pubblicati negli USA e numero di avvocati nello stato americano del Washington tra il 2005 e il 2009: indice di correlazione lineare = 0,93.
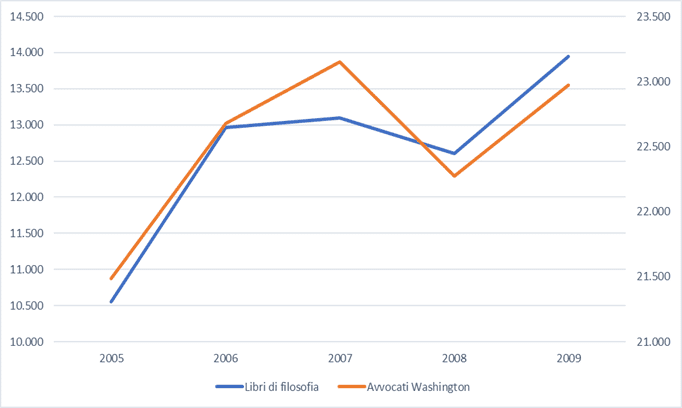
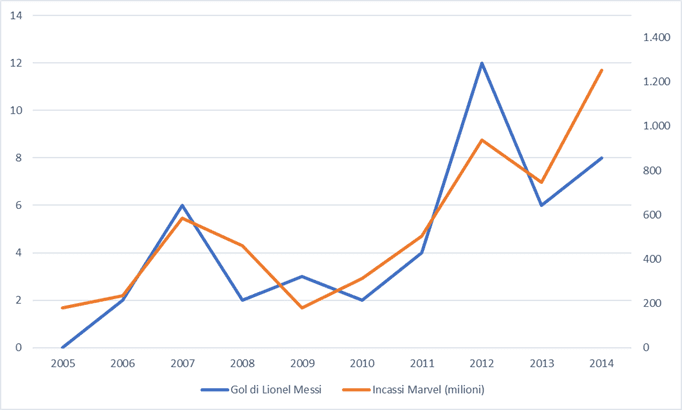
- Gol segnati da Lionel Messi nella nazionale Argentina e incassi dei film Marvel tra il 2005 e il 2014: indice di correlazione lineare = 0,84.
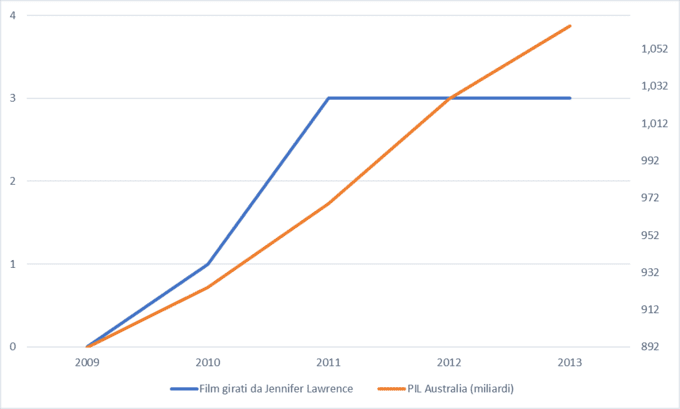
- Numero di film girati da Jennifer Lawrence e Prodotto Interno Lordo dell'Australia tra il 2009 e il 2013: indice di correlazione lineare = 0,88.
Chi fosse interessato a ulteriori coppie di variabili correlate in modo spurio, e ai link alle fonti dei dati utilizzati per la realizzazione di questi e di molti altri grafici del libro di Tyler Vigen, può visitare la seguente pagina: Spurious Book Sources.
Perché si verificano correlazioni così elevate tra variabili che non dovrebbero avere alcun legame tra loro?
Innanzitutto, perché le serie storiche sulle quali sono state misurate le correlazioni sono molto brevi.
Negli esempi appena visti sono stati utilizzati soltanto 5-10 anni di dati, quindi non più di 5-10 valori per variabile.
In secondo luogo, perché i già brevi periodi utilizzati sono stati selezionati ad hoc: basta modificarli e il valore dell'indice di correlazione varia drasticamente.
Ad esempio, se nella prima correlazione spuria si prendessero i dati tra il 2011 e il 2017, l'indice di correlazione passerebbe da 0,98 a −0,17: se nel secondo caso si spostasse la finestra temporale due anni in avanti, la correlazione scenderebbe da 0,95 a 0,59; se nell'ultimo caso, invece di prendere il quinquennio 2009-2013, si prendesse il 2013-2017, il valore dell'indice di correlazione crollerebbe da 0,88 a −0,72!
Quali conclusioni possiamo trarre dal fenomeno della correlazione spuria?
La più importante è quella che ogni correlazione lineare tra due serie di variabili deve essere analizzata a fondo, specialmente se la si vuole utilizzare a fini speculativi:
- Si potrebbe controllare quanto vari l'indice quando viene calcolato su serie storiche più lunghe o su diverse sezioni della medesima serie storica: se il valore dell'indice di correlazione è instabile, vuol dire che molto probabilmente non c'è alcuna causalità tra le variabili esaminate.
Il co-movimento è dovuto al caso e non esiste alcun motivo per cui debba continuare in futuro. - Deve esistere una motivazione economico-statistica alla base della correlazione lineare: la ricerca dovrebbe anzi partire da qui ed essere verificata in un secondo momento dal punto di vista statistico.
Nella realtà, le procedure di analisi viaggiano molto spesso in direzione opposta, salvo poi rendersi conto nel tempo che la presunta relazione tra le variabili era dovuta alla correlazione spuria.
Correlazione rolling

«The only thing that is constant is change».
Eraclito
La correlazione lineare tra due serie storiche di rendimenti finanziari non è costante. Se lo fosse, il lavoro degli statistici e degli analisti sarebbe molto più semplice ed efficace.
La correlazione lineare tende a modificarsi in base a due fattori:
- Il periodo di calcolo
- Il momento in cui avviene la misurazione
Per periodo di calcolo si intende la numerosità degli elementi delle serie storiche di cui vogliamo misurare la correlazione.
Se abbiamo a disposizione due serie storiche giornaliere, ci potrebbe interessare calcolare l'indice di correlazione lineare a 20 giorni, a 252 giorni o, magari, a 1000 o più giorni.
Gli indici calcolati assumeranno probabilmente valori molto diversi tra loro.
Il momento in cui avviene la misurazione corrisponde alla data di calcolo dell'indice. Come si vedrà meglio in seguito, l'indice di correlazione a 252 giorni calcolato, ad esempio, il 15 giugno 2004 potrebbe assumere un valore ben diverso da quello calcolato il 15 giugno 2015 sui rendimenti degli stessi due strumenti finanziari.
La correlazione rolling prevede il calcolo dell'indice di correlazione tra due serie storiche in modo ripetuto per tutto il periodo disponibile (serie storiche giornaliere nel nostro caso).
Ogni giorno, l'indice viene ricalcolato utilizzando le nuove informazioni disponibili (i due rendimenti più recenti), mentre quelle più datate vengono escluse. Un po' come avviene nel calcolo delle medie mobili (anche se in questo caso i calcoli vengono effettuati su una sola serie storica).
Prendiamo due fondi con serie storiche molto lunghe, a titolo esemplificativo: Eurizon EasyFund - Bond EUR Long Term LTE R e Anima Selezione Globale A.
Il primo è un fondo Obbligazionario Lungo Termine EUR mentre il secondo è un Azionario Internazionale Large Cap Blend.
Vediamo l'andamento del grafico delle correlazioni rolling a 252 giorni tra i rendimenti di questi due fondi. Il periodo analizzato va da gennaio 2000 a giugno 2019:
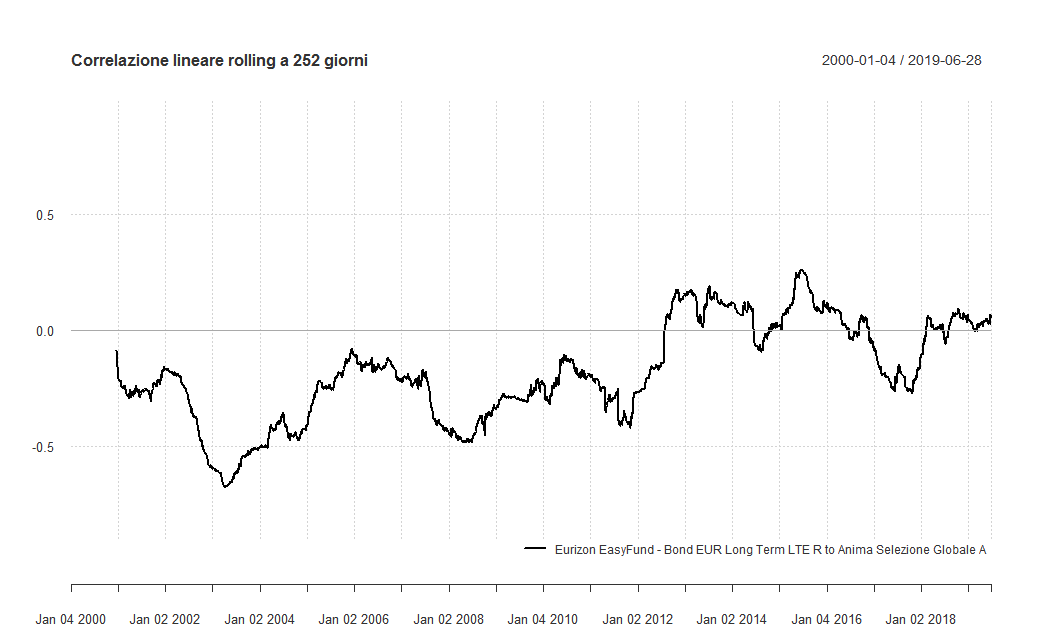
I valori dell'indice di correlazione lineare variano nel tempo in maniera abbastanza ampia seguendo trend ben identificabili a posteriori:
- In territorio negativo per oltre 10 anni, oscillando tra valori di poco sotto allo zero e inferiori a −0,60.
- Leggermente positivi per circa 4 anni, salvo per un breve periodo di qualche mese nel secondo semestre del 2014.
- Ancora negativi per un anno intero e poi di nuovi positivi ma molto vicini a zero.
Il valore minimo dell'indice è stato −0,68; quello massimo 0,26. Il valore medio dell'indice di correlazione in questi 18 anni e mezzo è stato −0,18. La standard deviation è stata pari a 0,21.
Ceteris paribus, vediamo adesso le correlazioni a 1260 giorni (5 anni circa):
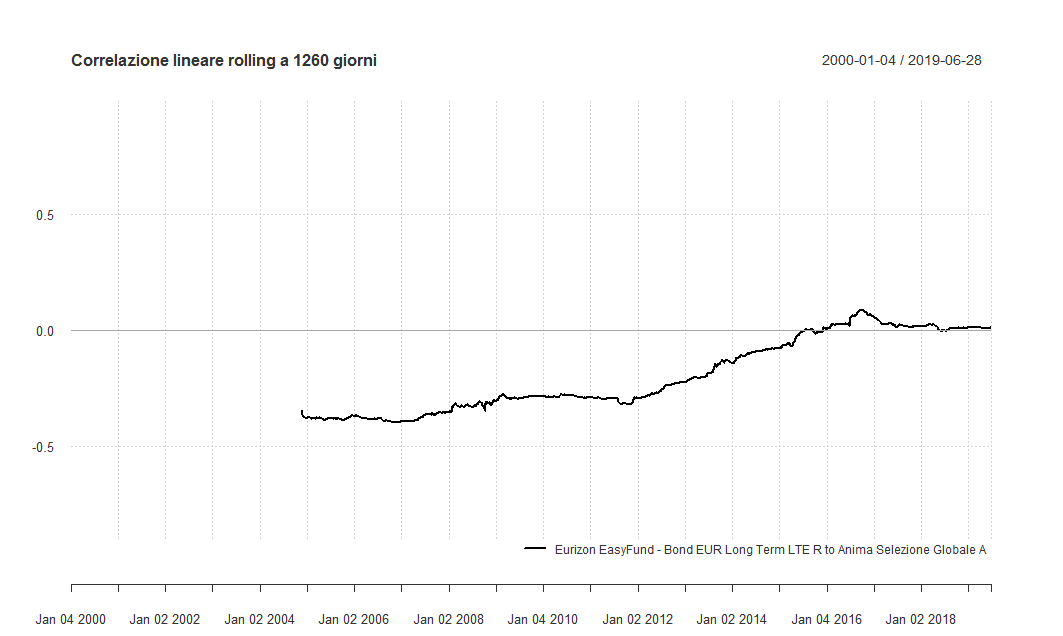
I valori dell'indice di correlazione si sono schiacciati verso lo 0 e la varianza è decisamente inferiore.
L'indice assume valori negativi per oltre 10 anni prima di diventare positivo e rimanere tale nei successivi 4 anni (seppure di poco superiore a 0).
Il valore minimo dell'indice è stato −0,40; quello massimo 0,09. Il valore medio dell'indice di correlazione in questi 14 anni e mezzo è stato −0,19. La standard deviation è stata pari a 0,16.
Aumentiamo ulteriormente il periodo di calcolo, portandolo a 2520 giorni (circa 10 anni). Ecco il grafico:
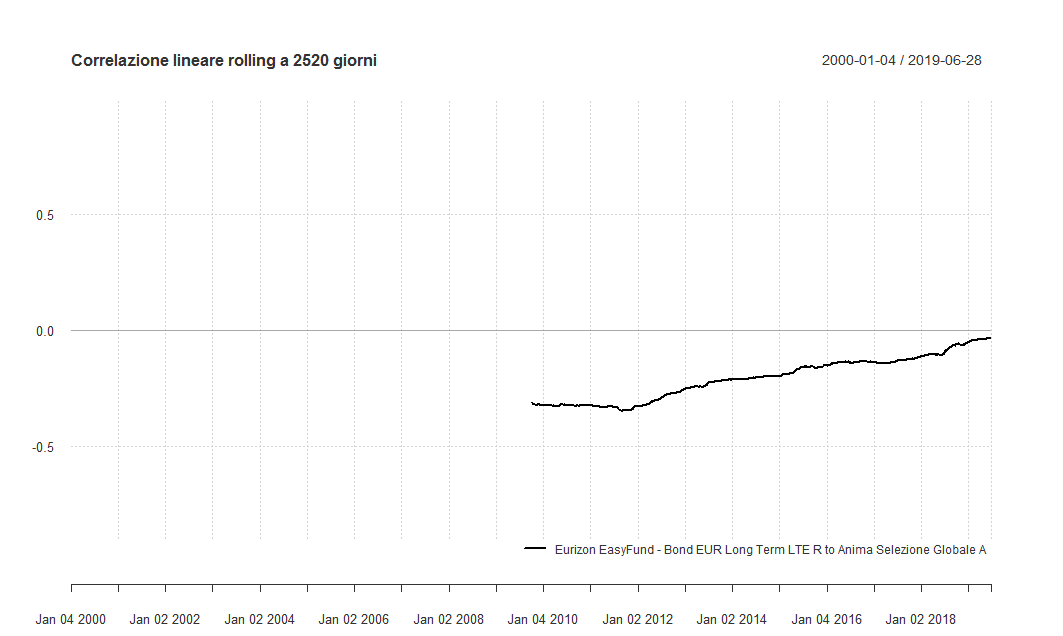
La distanza tra i valori massimi e minimi è diminuita ulteriormente. Anche la varianza si è ridotta.
L'indice di correlazione non è mai stato positivo, anche se il trend è stato crescente (gli ultimi valori sono di poco inferiori allo 0).
Il suo valore minimo è stato −0,35; quello massimo −0,03. Il valore medio dell'indice di correlazione in questi 9 anni e mezzo è stato −0,21. La standard deviation è stata pari a 0,09.
Come varia, invece, l'indice di correlazione calcolato su periodi brevi?
Vediamo quello a 20 giorni:
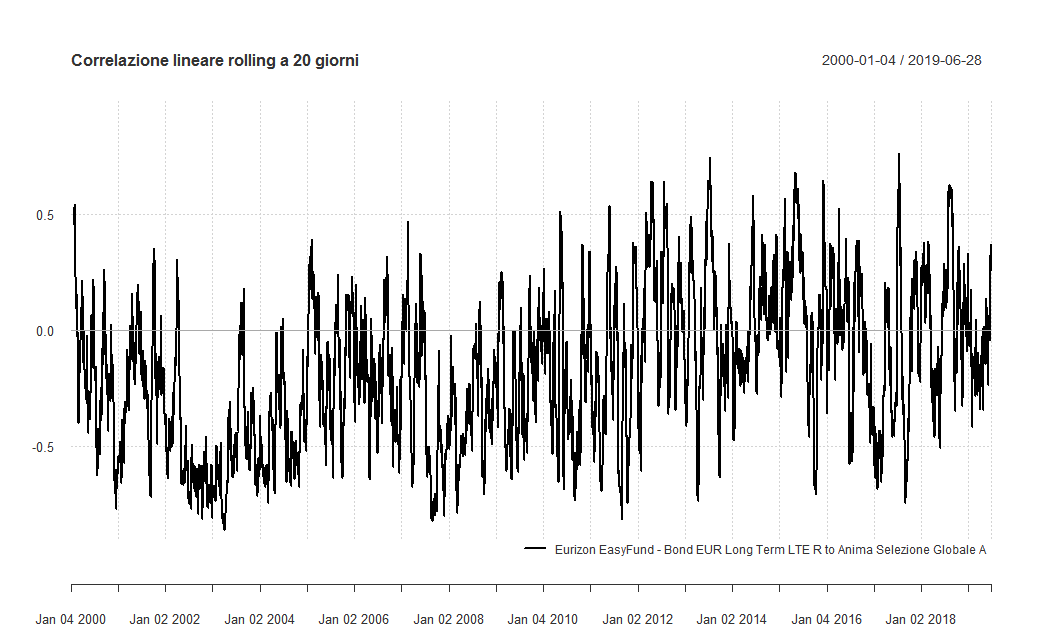
Il grafico è molto più difficile da decifrare. Le oscillazioni sono estreme e non è possibile identificare dei trend.
Sembra che l'indice di correlazione calcolato su periodi così brevi (20 giorni è poco meno di un mese) non fornisca informazioni utili e non sia altro che una misurazione della correlazione tra il rumore (noise) delle due serie storiche.
Il valore minimo dell'indice è stato −0,86; quello massimo 0,77. Il valore medio dell'indice di correlazione in questi 19 anni e mezzo è stato −0,18. La standard deviation è stata pari a 0,33.
Si può concludere ribadendo come sia la lunghezza del periodo scelto per il calcolo dell'indice di correlazione, sia il momento in cui avviene la misurazione, ne influenzino il valore.
In particolare, più il periodo di calcolo è breve e più grandi e frequenti saranno le oscillazioni dell'indice.
Si dovrà perciò fare molta attenzione alla scelta della lunghezza del periodo di calcolo dell'indice di correlazione e, nel caso in cui lo si voglia utilizzare operativamente, sarà bene non scegliere periodi troppo brevi: è molto probabile che il suo valore cambi troppo velocemente per essere sfruttato in modo profittevole.
Analisi di correlazione lineare di Dedalo Invest

«There is zero correlation between IQ and emotional empathy... They're controlled by different parts of the brain».
Daniel Goleman
Dedalo Invest permette di calcolare l'indice di correlazione lineare tra due o più serie storiche finanziarie.
Nell'output della nostra Analisi di correlazione lineare potrete notare che, indipendentemente dal tipo di analisi scelta, verranno visualizzate due serie di risultati: correlazione dei rendimenti e correlazione dei NAV dei fondi.
In un'ottica di gestione del portafoglio la correlazione dei rendimenti è quella rilevante.
Le differenze sono talvolta notevoli: questi gap sono riconducibili all'assenza di invarianza della correlazione in seguito a trasformazioni non lineari strettamente crescenti.
In linea generale, si può infatti affermare che:
corr(T(X), T(Y)) ≠ corr(X, Y)
Senza entrare troppo in tecnicismi, questo significa che i rendimenti di due fondi potrebbero non essere correlati mentre i prezzi potrebbero essere fortemente correlati (o viceversa).
Come è noto, l'indice di correlazione è sempre compreso tra −1 e +1. Quello che pochi sanno è che questo intervallo di valori è valido soltanto se le variabili casuali misurate seguono una distribuzione normale o t multivariata.
Su questa ipotesi si basano implicitamente molte delle applicazioni che ricevono in input le serie storiche dei rendimenti degli strumenti finanziari.
Tuttavia, essa non è necessariamente vera e tanto più le distribuzioni reali dei dati si allontanano dalle due citate, tanto più i limiti di −1 e +1 perdono di significato e possono anche essere irraggiungibili.
Ad esempio, se X e Y sono variabili casuali distribuite log-normalmente invece che normalmente, non sarà possibile che l'indice di correlazione lineare assuma determinati valori.
Se ipotizziamo che ln(X) segua una distribuzione normale standardizzata e ln(Y) una normale con media 0 e varianza 4 – N(0, 4) – allora l'indice di correlazione lineare non potrà mai superare il valore di 2/3 e non potrà mai essere inferiore a –0,09: sono dei valori ben lontani dai classici +1 e −1.
Nonostante tutti i suoi limiti, l'indice di correlazione lineare rimane una misura statistica molto utilizzata, capace di fornire informazioni fondamentali in un'ottica di gestione del portafoglio.
Le analisi disponibili su Dedalo Invest possono essere effettuate tra singoli strumenti finanziari (fondo-fondo, fondo-indice, fondo-tasso di interesse e fondo-tasso di cambio), ma anche tra tutti i fondi di una o due diverse categorie o tra un elevato numero di indici: anche diverse migliaia di correlazioni per volta.
Di conseguenza, l'analisi potrebbe richiedere un tempo di calcolo relativamente alto e un po' di pazienza: l'output generato, però, fornisce una straordinaria quantità di informazioni.
Qui di seguito vengono visualizzate alcune sezioni della tabella di output dell'analisi di correlazione lineare. Negli esempi sono riportati dei fondi a gestione attiva, ma l'analisi include anche tutti gli ETF presenti nel nostro database:
| Primo fondo | Secondo fondo | Correlazione lineare dei rendimenti | Correlazione lineare dei NAV/valori | Differenza di rendimento |
|---|---|---|---|---|
| Schroder ISF - Italian Equity A Acc | Schroder ISF - Italian Equity C Acc | 1.00000 | 0.99983 | −0.44% |
| AXA World Funds - Framlington Italy AC EUR | AXA World Funds - Framlington Italy FC EUR | 0.99999 | 0.99958 | −0.63% |
| CS (Lux) - Italy Equity B EUR | CS (Lux) - Italy Equity IB EUR | 0.99999 | 0.99877 | −1.03% |
| Schroder ISF - Italian Equity A Acc | Schroder ISF - Italian Equity C Acc | 0.99999 | 0.99983 | −0.44% |
| Fonditalia Equity Italy R | Fonditalia Equity Italy T | 0.99999 | 0.99956 | −0.55% |
| Zenit Multistrategy Stock Picking I Acc | Zenit Multistrategy Stock Picking P Acc | 0.99999 | 0.99990 | 0.59% |
Estratto delle prime 6 coppie di fondi nell'output di Analisi di Correlazione Lineare (categoria Azionari Italia).
| Primo fondo | Secondo fondo | Correlazione lineare dei rendimenti | Correlazione lineare dei NAV/valori | Differenza di rendimento |
|---|---|---|---|---|
| Eurizon EasyFund - Equity Italy LTE R | OYSTER Italian Value C EUR PF | 0.71606 | 0.91064 | −1.49% |
| OYSTER Italian Value C EUR PF | Symphonia Azionario Small Cap Italia I | 0.71132 | 0.71132 | −0.88% |
| OYSTER Italian Value C EUR PF | iShares - FTSE MIB UCITS ETF (Acc) (EUR) | 0.70876 | 0.85846 | −0.84% |
| iShares - FTSE MIB UCITS ETF (Acc) (EUR) | iShares - MSCI Italy Capped ETF (USD) | 0.69869 | 0.93797 | 5.54% |
| Lemanik SICAV High Growth Capitalisation Institutional EUR | iShares - MSCI Italy Capped ETF (USD) | 0.69573 | 0.93905 | 3.79% |
| Fidelity Funds - Italy E-Acc-EUR | iShares - MSCI Italy Capped ETF (USD) | 0.69568 | 0.94270 | 1.57% |
Estratto di 6 coppie di fondi nella parte centrale dell'output di Analisi di Correlazione Lineare (categoria Azionari Italia).
| Primo fondo | Secondo fondo | Correlazione lineare dei rendimenti | Correlazione lineare dei NAV/valori | Differenza di rendimento |
|---|---|---|---|---|
| BG Selection SICAV - Anima Italy Equities AX | Anima Geo Italia A | 0.07748 | 0.91022 | −5.70% |
| Atlante Target Italy A Acc | BG Selection SICAV - Anima Italy Equities AX | 0.07699 | 0.93830 | −5.46% |
| Allianz Azioni Italia All Stars | BG Selection SICAV - Anima Italy Equities AX | 0.07489 | 0.97277 | −3.99% |
| Anima Italia A | BG Selection SICAV - Anima Italy Equities AX | 0.07420 | 0.91527 | 4.58% |
| BG Selection SICAV - Anima Italy Equities AX | Piano Azioni Italia A | 0.07207 | 0.96814 | 2.33% |
| AXA World Funds - Framlington Italy FC EUR | BG Selection SICAV - Anima Italy Equities AX | 0.06856 | 0.95249 | −1.64% |
Estratto di 6 coppie di fondi della parte inferiore dell'output di Analisi di Correlazione Lineare (categoria Azionari Italia).
Le correlazioni lineari di queste 18 coppie di fondi rappresentano una minima parte dell'output generato dall'analisi di correlazione lineare a 252 giorni tra tutti i fondi della categoria Azionari Italia.
Nella sua interezza, l'output sarebbe stato composto da più di 1.400 coppie di fondi.
Ogni analisi può infine essere personalizzata in base ai parametri descritti nel paragrafo seguente.
Parametri dell' analisi di correlazione lineare

«It's a wonderful thing, as a writer, to be given parameters and walls and barriers».
Neil Gaiman
Tipo di analisi: si possono effettuare 6 tipi di analisi di correlazione lineare:
- Analisi singole:
- Tra due fondi specifici.
- Tra un fondo e un indice.
- Tra un fondo e un tasso di interesse.
- Tra un fondo e un tasso di cambio.
- Analisi multiple:
- Tra tutti i fondi di una o due categorie.
- Tra tutti gli indici.
Periodo (in giorni): periodi di calcolo dell'analisi di correlazione lineare. Non deve essere inferiore a 5 giorni.
Giorni finali: Numero di giorni che vengono tolti alla fine di tutte le serie storiche prima di calcolare le correlazioni. Serve a evitare che alcune serie abbiano valori non aggiornati (il NAV di alcuni fondi è disponibile soltanto uno o più giorni dopo).
Media periodi: Utilizzazione della media di 3 periodi a scelta dell'utente – invece che di un periodo singolo – nel calcolo della correlazione lineare.


